1 二叉搜索树
基础API:
bool get(Key key, Value& val); // 查找key对应的value
bool put(Key key, Value val); // 插入或更新key对应的value
bool remove(Key key); // 删除指定key
查找
二叉搜索树本身是维护了有序性:一个节点的值总是大于左子树所有节点的值,小于右子树所有节点的值。
此外,二叉搜索树本身包含了递归的思想:任何一棵树,都是由 根节点 + 左子树 + 右子树 构成。
Node* get(Node* node, Key key)
{
if(node == NULL)
return NULL;
if(node->key == key)
return node;
if(node->key < key)
return get(node->right, key);
else
return get(node->left, key);
}
删除
二叉树的删除操作:
- 如果删除的节点是叶子节点,直接删除即可;
- 如果删除的节点只有一个子树(左或者右),直接将子树提上来即可;
- 如果删除的节点有两个子树,那么将它的后继节点,也就是右子树的最小节点提上来,然后将其从右子树删除即可。
注:将一个节点A提到节点B的位置,只需要将A的value赋值到B即可,然后将节点A删除即可。如果是要将节点B的父节点指向节点A来替换的话,那必须修改节点B的父节点的信息,比较麻烦。
如何删除一个树最小的节点:
// 删除node为根节点的树中最小的节点,并返回新的根节点
Node* deleteMin(Node* node)
{
if(!node)
return NULL;
if(node->left) {
node->left = deleteMin(node->left);
} else {
Node* right = node->right;
delete node;
node = node->right;
}
return node;
}
2 红黑树
红黑树是2-3-4树的等价。一颗2-3-4树有如下性质:
- 每个节点最多可以存储3个key,并按顺序排列;
- 所有的叶子节点(没有儿子节点的节点)都在同一个level(到树根的距离);
- 所有的非叶子节点可能是:
- 2-节点:存储1个key,有两个(非空的)儿子节点;
- 3-节点:存储2个key,有3个(非空的)儿子节点;
- 4-节点:存储3个key,有4个(非空的)儿子节点。
- 所有的叶子节点可能有1,2或者3个key,没有儿子节点。
可以看到,2-3-4树的性质保证了,查找任何一个key,其最大比较次数为O(logN)。但是2-3-4树实现起来比较麻烦,需要定义3种类型的node。
红黑树通过将二叉树中的节点着色,就可以等价表示任何一颗2-3-4树。只有在删除或插入时需要维护颜色信息以保证2-3-4树的平衡,在查找时它就是一颗普通的二叉树。所以在工程上,一般是使用红黑树来替换2-3-4树。
红黑树与2-3-4树的等价表示
在红黑树中,一个红色的节点,表示它与它的父节点在同一个2-3-4树的节点中。所以,2-节点,3-节点,4-节点在红黑树中分别表示如下:
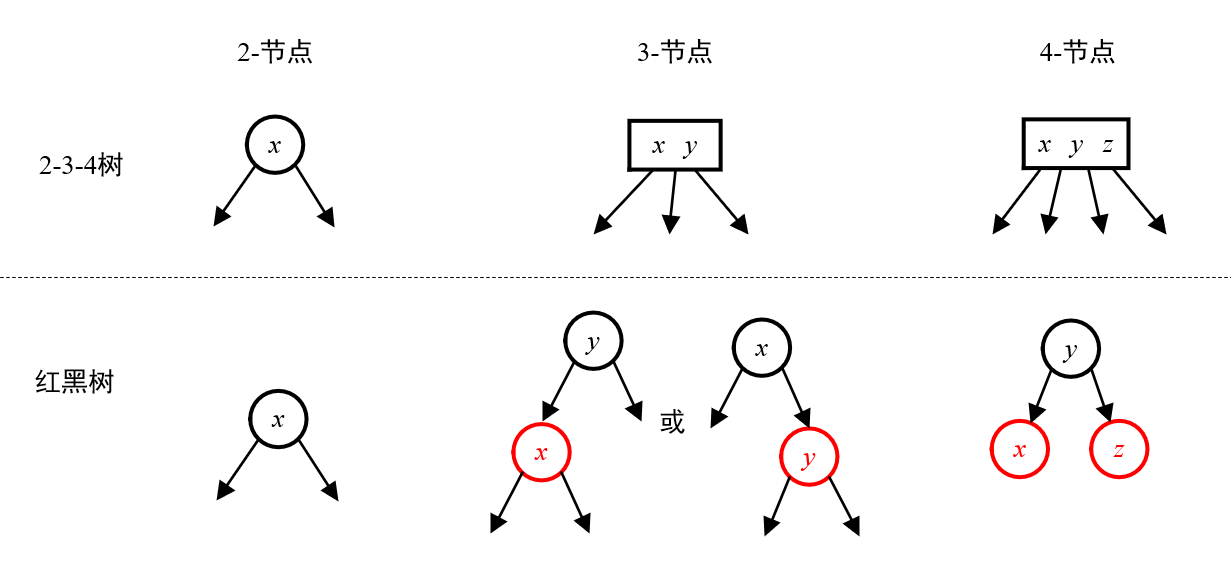
所以,根据2-3-4树的性质,我们可以得出红黑树需要具备如下性质:
- 首先,它是一颗二叉搜索树,每个节点最多存储1个key,最多可以有1个或2个子节点;
- 每个节点要么是黑色的,要么是红色的;
- 根节点是黑色的,NIL节点按黑色算;
- 如果一个节点是红色的,那么它的儿子节点必须是黑色的;
- 每个NIL节点到根节点的路径上,黑色节点的个数必须相等;
插入
删除
3 B树
B树是满足如下性质的搜索树:
- 每个节点可以包含多个key。根节点最少包含1个key;内部节点key数量由树的最小度数
t决定,节点数在[t-1, 2t-1]范围内; - 如果内部节点有
n个key,那么它有n+1个子节点。每个子节点中的key的范围由父节点中对应 该子树 的key来界定; - 每个叶子节点具有相同的深度,即树的高度
h。
可以看到,当B树的最小度数t=2时,它就是一颗2-3-4树。
当然,实际使用时,B树的t一般都很大,用来作为磁盘存储的数据结构:通常一个节点存储的数据,在磁盘中对应一次读写操作返回的数据。这样,一棵高度为h的B树,它的一次查找操作最大的读磁盘次数就是O(h)。
考虑当t=1000时,存储1亿个key的B树,它的高度也才等于3。
B树的插入和删除操作的原理,类似于2-3-4树。只不过在实现中,一般使用自顶向下的调整方法。