1 如何在2-3-4树中插入数据
在2-3-4树中,新key总是插入到树的叶子节点中(也就是最底层)。根据key的顺序我们可以根据查找路径到达合适的叶子节点。
Case 1: 叶子节点是2-节点或者3-节点
直接将新key插入进去,变成3-节点或4-节点即可。
Case 2: 叶子节点是4-节点
此时已经没有空位来插入新key了,不然它就会变成了一个”5-“节点,这是不合法的。
我们可以将4-节点的中位key往上移,将它放进它的父节点中,然后将剩下的两个key拆分成2个2-节点,这样就可以把key放入合适的那个2-节点了!
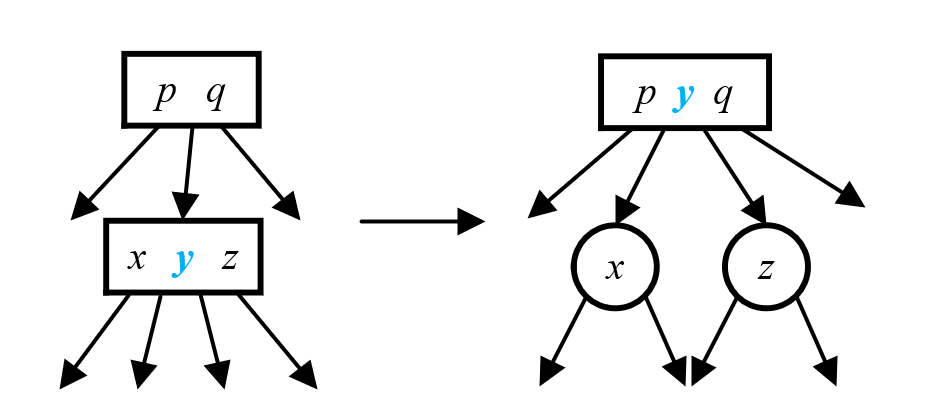
- 如果父节点是2-节点或3-节点(如上图所示),那完美!
- 如果父节点是4-节点,那就重复刚刚的操作,将父节点的中位key再往上移,空出一个位子给下面上来的key!
可以看到,如果是往4-节点插入key,会引起中位key一直往上移来给下面上来的key腾位置,直到遇到一个非4-节点,或者到达根部!
如果到了根部之后发现根部也是一个4-节点,那就将根部的中位key向上移动变成一个独立的2-节点,并成为新的根部。这也是2-3-4树长高的唯一方式。
2 在红黑树中实现插入算法
从上面的算法描述上看,我们的插入操作发生在树底部,然后自底向上重新调整树以维持平衡性。
下面我们就在红黑树上实现该算法。
rbt_node* __rbtree_put(rbt_node* node, int key, char* value)
{
if(node == NULL) {
return __rbtree_new_node(key, value);
}
if(node->key == key) {
node->value = value;
return node;
}
if(node->key > key) {
node->left = __rbtree_put(node->left, key, value);
} else {
node->right = __rbtree_put(node->right, key, value);
}
/* 这里重新调整树 */
}
我们实现了一个递归函数__rbtree_put来完成插入功能。函数负责将指定的key插入到以node为根的树中,并返回插入后树的根节点。
首先,我们将key与根节点做比较,如果比根节点小,那就递归地插入到左子树中,并更新插入后左子树的root;反之比根节点大,那就插入到右子树中。
最终会到达某个叶子节点,它的左节点或者右节点为空,这时候我们会为待插入的key新创建一个节点,初始颜色为红色,并将它挂到叶子节点上。
从红黑树的性质来说,新插入一个节点,它的初始颜色是红色,所以它不会违反黑节点长度的性质,它只会违反“红色节点不能连续”的性质。为什么红黑树要有这条性质要求,因为我们在定义红黑树跟2-3-4树的转换规则时,4-节点只有一种合法形式,其它形式都有个特点就是2个红色节点连续,所以规定红黑树不能有红色节点连续,这样就确定了4-节点的表示形式的唯一。
所以,这里需要确认一点:从红黑树的角度来说,我们之所以要在子树的插入完成后对树进行调整,不是因为插入了新节点,而是原本黑色的子节点可能变成了红色。
根据上一节的算法描述,在从根部到叶子节点的整条路径上的所有节点都有可能需要做调整。所以我们在递归函数中,完成子节点的插入后,需要重新调整树。
Case 1: 往3-节点插入key
虽然说在2-3-4树中可以直接往3-节点插入新key而无需调整,但是在红黑树中,需要避免一种情况:可能会出现连续的红节点,如下图所示:
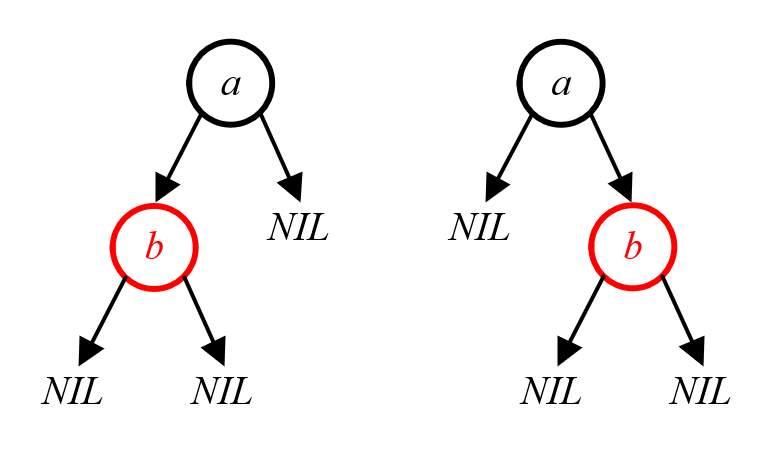
如果新key成为节点b的子节点的话,就会出现连续的红色节点,
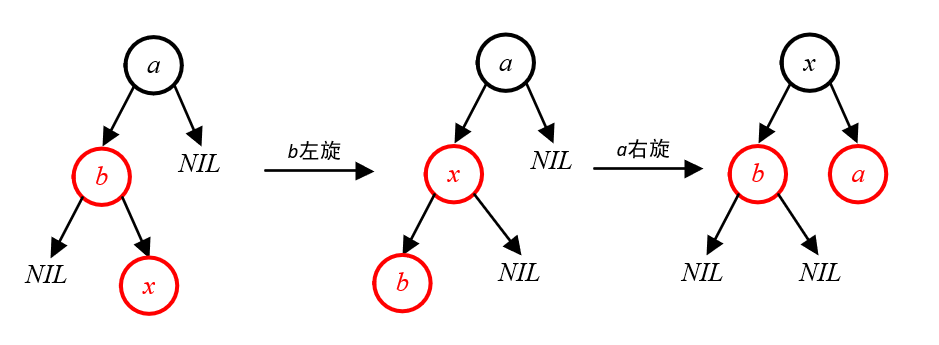
具体处理过程如上图所示,如果是左图的形式,先对b进行右旋,转变成中图的形式,然后再对a进行左旋,就变成了合法的4-节点形式了。
当b在a右侧时,处理方法跟上面是镜像关系:先对b进行左旋,再对a进行右旋。
Case 2: 往4-节点中插入key
4-节点只有一种形式,但是插入的x的位置可能有4种:a左,a右,c左,c右。
在上节的算法描述中,我们说到,要把4-节点拆分成2个2-节点并把中位key上移到父节点中。这个听起来很复杂的操作,其实在红黑树中很好实现:只需要把b的颜色变成红色,a和c的颜色变成黑色,即可。
完成颜色翻转后,4种情况下x的父节点都是黑色了,都不需要额外处理了。
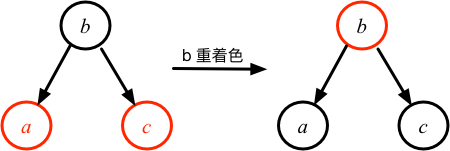
回到我们刚刚说的为什么要调整红黑树的问题上,这里我们把原来是黑节点的b,变成了红色,所以对于b的父节点,它就需要相同的调整过程,因为它的父节点有可能是2-节点,3节点或者4-节点。
代码实现
以下就是上面描述的调整算法的具体实现了,对照着图示阅读代码效果更佳。
/* 我们在node为新的红色节点的爷爷节点上处理 */
/* 先处理新的红色节点在node->left上*/
/* 先处理新的红节点在node->left->right的情况,如果(node,node->left,node->right)是4-节点,
直接翻转颜色;如果是3-节点,先对node->left左旋,使红节点变成在node->left->left */
if(__rbtree_is_red(node->left) && __rbtree_is_red(node->left->right)) {
if(__rbtree_is_red(node->right)) {
__rbtree_flip_colors(node);
} else {
node->left = __rbtree_rotate_left(node->left);
}
}
/* 再处理新的红节点在node->left->left的情况,如果(node,node->left,node->right)是4-节点,
直接翻转颜色;如果是3-节点,对node进行右旋*/
if(__rbtree_is_red(node->left) && __rbtree_is_red(node->left->left)) {
if(__rbtree_is_red(node->right)) {
__rbtree_flip_colors(node);
} else {
node = __rbtree_rotate_right(node);
}
}
/* 再处理新的红色节点在node->right上。将上面的2个if中的left换成right,right换成left即可 */
实现了内部函数__rbtree_put后,我们对根节点调用该函数即可。
int rbtree_put(rbtree_t* rbt, int key, char* value)
{
rbt->root = __rbtree_put(rbt->root, key, value);
rbt->root->color = RBT_BLACK;
return 0;
}
如果根节点本身就是4-节点(root为黑,root->left和root->right为红),那么最终会分解成2-节点,此时在算法中root->left和root->right变成黑色,root变成红色。由于根节点没有父节点去处理它,所以我们直接把根节点重置为黑色即可。
关于红黑树的插入算法,就写到这里了。删除操作请参考红黑树上的删除操作