1 在2-3-4树中删除key
跟二叉树一样,如果要被删除的key不在叶子节点,那么我们将其与它的后继节点交换,这样确保被删除的key总是在叶子节点中。
在2-3-4树中,我们要删除一个叶子节点中的key,有3种情况:
- 被删除的key是一个2-节点;
- 被删除的key在一个3-节点中;
- 被删除的key在一个4-节点中。
对于3-节点或4-节点,我们可以直接删除,使其变成2-节点或3-节点。但是对于2-节点,如果被删除了,那就会违反“所有叶子节点到根节点距离相等”的性质。
我们有两种思路去解决这个问题:
- 自顶向下
- 自底向上
自顶向下
我们在从根节点向下查找被删除key的过程中,如果碰到2-节点,将其调整为3-节点或4-节点。这样,最后到达被删除的key时,它就不可能是2-节点了。
下面就介绍一下在自顶向下的过程中如何“消除”2-节点。
从兄弟节点借
如果兄弟节点是3-节点或者4-节点,我们可以从兄弟节点借1个key过来。为了保证顺序性,我们不能直接把兄弟节点中的key从(父节点的)一边移到2-节点的一边。通常我们是将父节点中的key下移到2-节点,再将兄弟节点中的key上移到父节点。这个操作我们称为“旋转”。
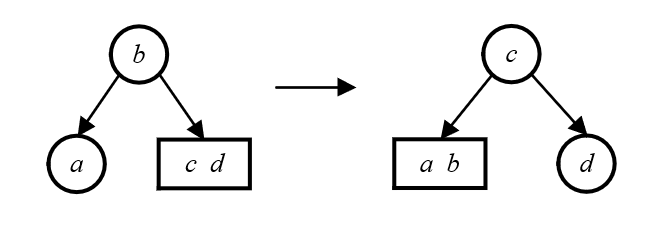
从父节点借
如果兄弟节点也是2-节点,怎么办?
先考虑父节点是3-节点或4-节点的情况。我们将父节点中相应的key、兄弟节点和待消除2-节点,合并成一个4-节点。
如果父节点也是2-节点,这只会发生在根节点:因为我们在自顶向下时已经把所有2-节点都消除了。
对于根节点、其左子节点、其右子节点都为2-节点的情况,我们直接将这3个节点,合并成一个4-节点。这样整棵2-3-4树的高度就减1了。
自底向上
与自顶向下不同,在从上往下查找过程中不做任何调整,直到到达底部,将目标key删除后,再从下往上调整树。
要处理的case类似:
- 如果被删除的key在3-节点或4-节点中,调整结束。
- 如果被删除的key是2-节点,看兄弟节点:
- 如果兄弟节点是3-节点或4-节点,从兄弟节点移一个key过来填坑,调整结束;
- 如果兄弟节点是2-节点,将父节点移下来和兄弟节点合并成一个3-节点来填坑。再对父节点重复以上调整过程。
最终,在向上调整过程中要么到达某个节点后结束,要么直到根部,然后树高度减1。
2 红黑树中的实现
我们将上述2-3-4树中的算法,用红黑树表示之后,仔细列出各种case然后针对处理即可,这里不再详述算法过程,也不方便理解。
具体算法请看rbtree.c
上述实现是采用的自底向上调整算法,自顶向下相对更容易点。